Q.1 State the first law of thermodynamics
Ans. First law of thermodynamics states that, “If a system passes through a cycle of processes so that it returns to its initial state the sum of heat and work effects will be zero
Q.2 What is mechanical equivalent of heat?
Ans. Joule conducted a number of experiments involving various types of work interactions and found out that
Where J is known as Joule’s equivalent or mechanical equivalent of heat.
Q.3. Represent the following processes on P-V and T-S diagrams:
(I) Constant pressure process (ii) Adiabatic process.
Q. 4. Represent the following processes on P-V and T-S diagram.
(i) Constant volume process (ii) Constant temperature process.
Q. 5. For generation of steam in a boiler requires 2500 kJ/kg of heat and in the condenser 1800 kJ/kg of heat is rejected to cooling water, using first law of thermodynamics, determine steam flow rate.
Ans. h1 = 2500 kJ/kg, h2 = 1800 kJ/kg
Steam flow rate = h1 — h2 = 2500 — 1800 = 700 kJ/kg.
Q. 6. What is non-flow process?
Ans. The processes taking place in a closed system which do not permit the transfer of mass across their boundaries are known as non-flow processes.
Q.7. What is an isobaric process?
Ans. In an isobaric process, both volume and temperature change, where as pressure is kept constant. The volume and temperature increases when heat is supplied to system and decreases when heat is rejected by the system.
Q.8. Represent isothermal and adiabatic processes on p-v chart.
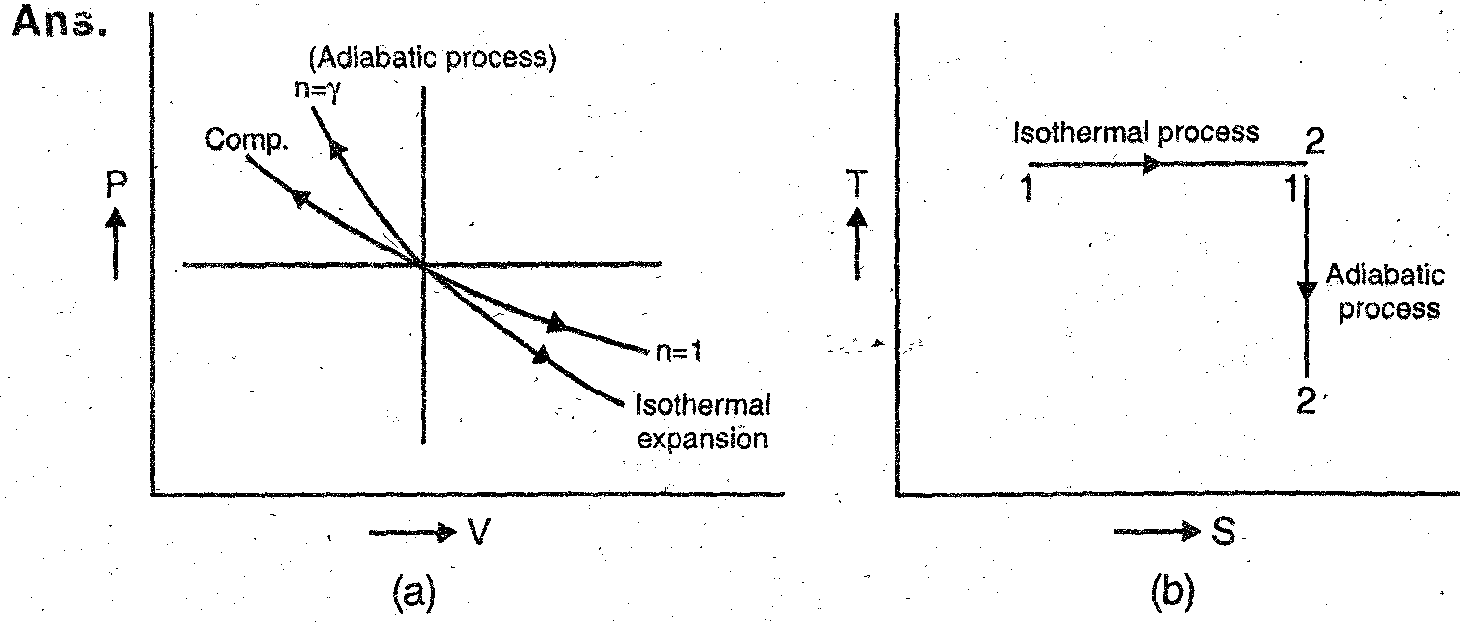
Q 9. Why a hyperbolic process is similar to constant temperature process in the
case of gases.
Ans. The plot of a rectangular hyperbola is represented by pV = C. Since the law of an isothermal process is also the same i.e. pV = C, therefore it follows that in the case of gases, the isothermal and hyperbolic processes are same. Hence the equations derived for work, heat and change in internal energy for on isothermal and hyperbolic process are also same.
[Long Questions]
Q 1. (a) Derive an expression for heat transfer and work done for an isothermal
process.
(b) Air enters a compressor at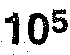 
Pa and 25°C having volume of 1.8 m
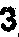/kg and is compressed to 5 x 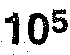Pa isothermally, determine (i) Work done (ii) Change in internal energy (iii) Heat transferred,
Ans. (a) Isothermal process is a process of expansion and compression of a gas during which temperature of gas remains constant. There is no change of internal energy and enthalpy remains constant. Fig
Where K is a constant of proportionality
Using (2) in (1)
But, if, PV = P1V1 = P2V2
Where r is called the expansion ratio.
W.D will be negative when isothermal compression takes place and r in this case will be called compression ratio.
Heat transferred:
Now, in an isothermal process
dU = 0
This means a heat supplied gets converted into work during an isothermal process.
(b) Given:
In an isothermal process from 1 — 2, refer Fig.
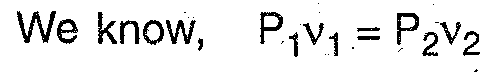
Change in internal energy, dU = U2 — U1 = 0
according to 1st law of thermodynamics,
Since dU=0
Q 2. Air undergoes a cyclic process in a cylinder and piston arrangement. First the
atmospheric air at 1 bar and 27°C is compressed adiabatically to 10 bar, then expanded isothermally upto initial condition under constant pressure, find out (a) Change in internal energy (b) Change in enthalpy (c) Heat transfer (d) Work transfer for each process and also for the cycle.
From Fig.
Adiabatic Compression1—2:
Isothermal expansion (2—3)
P2V2 = mRT2
substituting the value of V2 in equation (1),
Also during isothermal process,
P2V2 = P3V3
Constant pressure process: (3—1 )
Heat transfer:
Total work done during the complete cycle,
Q.3.One kg of air at 1 bar and 300 K is compressed adiabatically till its pressure becomes 5 times the original pressure. Then its expanded at constant pressure and finally cooled at constant volume to return to its original conditions, calculate:
(a) heat transfer (b) work transfer (c) internal energy for each process and for the cycle. Represent the process as PV and T-S diagrams.
Process 1—2 (adabatic process):
m = l kg
P1 = 1bar, T1 = 300K
P2 = 5bar
From characteristic gas equation
P1V1 = mRT1
Process 2—3 (Constant Pressure process):
Process 3—1 (Constant volume process)
Change in internal energy,
Total work done in cycle:
Since internal energy is a property so its cyclic integral will be zero
Q.4 Define enthalpy. How does it differ from heat’ Prove that heat exchange for isobaric process is equal to change in enthalpy
Ans. Enthalpy The sum of internal energy and displacement work (pressure volume)
of the given quantity of gas is called enthalpy and is denoted by H.
On the other hand heat is a form of energy that is transferred (without transfer of
mass) across the boundary of system because of temperature difference between the system and surroundings It is denoted by Q and expressed in joule (J)
Heat exchange for an isobaric process:
Q=mC(T2 - T1)
also from 1st law of thermodynamics,
Which is equal to the increase in enthalpy
Q.5 During a process, the temperature of system rises from 100°C to 200°C Heat transfer per degree rise in temperature at each temperature reached during the process is given by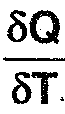 
= 1.005 kJ/K The work done on system per degree rise in temperature at each temperature reached is given by = (4— 0.12T) kJ/K. Calculate the change in internal energy of system during the system.
Q. 6. 200 litres of air at 4 bar and 400 K is contained in a system. A reversible adiabatic expansion takes place till the pressure falls to I bar. The gas is then heated at constant pressure till the enthalpy increases of 72 kJ. Calculate: (a) The work done (b) Index of expansion if the above processes are replaced by a single reversible polytropic process giving the same work between same initial and final states. Take Cp = 1 kJ/kg K and Cv = 0.714 kJ/kg K.
Ans.
From Fig. 8
Process 1—2 (Adiabatic process):
Mass of gas:
Process 2—3 constant pressure heating:
Total work done during the process .1—2—3,
Index of expansion:
If the entire work is done by a polytropic process, then
Q.7. Distinguish between different polytropic processes, draw common P-V diagram showing expression, following the law 
= C for n = 0, n = 1 and n = ‘n’.
Constant volume process or isotropic process.
Fig. shows all the above processes.
The Fig. shows the curves of expansion and compression of a perfect gas for different values of in. It is clear that higher the value of n, steeper is the curve of expansion or compression.
Q.8. 3kg of air kept at an absolute pressure of 100 kPa and temperature of 300 K is compressed polytropically until the pressure and temperature becomes 1500 kPa and 500 K respectively. Evaluate the polytropic exponent, the final volume and the work of compression. Take, gas constant R = 287 J/kg K
Ans. Given: m = 3 kg
P1= 100 kPa,
T1= 300K
R = 287 J/kg K
For a polytropic process,
Taking log on both sides.
Work of compression,
Q. 9. Explain the first law of thermodynamics. Draw P-V diagram for the cyclic process.
Ans. According to first law of thermodynamics, total energy of a system in all its forms remains constant”
These are other statements of 1st law of thermodynamics which are as follows
1. Heat and work are inter convertible. When a system undergoes a thermodynamic- cycle then the net heat supplied to the system from the surroundings is equal to not work done by system on its surroundings.
or “Cyclic integral of work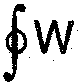 
must be equal to cyclic integral of heat 
, both forms of energy being expressed in same units”
2. Energy can be created nor destroyed, but one of form of energy can be transformed
to other form.
Corollaries of 1st law of thermodynamics:
1. If a system is taken through a cycle of processes so that it returns to the same state or conditions from which it started, the sum of heat and work effects will be zero.”
Also, when a system executes a process, the change in stored energy of system is numerically equal to net heat interaction minus the net work interaction during the process.
2. The energy of an isolated system is always constant.
An isolated system is one in which there is no energy no mass transfer of system with the with surroundings.
For an isolated system,
dE = 0
or E = Constant.
3. A perpetual motion machine of first kind is impossible. (Fig.)
First law of thermodynamics applied to a cyclic process:
Considering a closed system which undergoes a series of processes which make a cycle as shown in fig.
Let the processes be represented by 1—2, 2—3, 3—4 and 4—1. According to 1st law of thermodynamics,
For process 1—2,
On adding (1), (2), (3) and (4) equations,
We get heat interactions for cycle is equal to work interactions for cycle.
Above equations shows that for a closed system undergoing a cyclic process, then the cyclic integral is equal to the cyclic integral of work
Q.10. 0.44 kg of air at 180°C expands adiabatically to three times its original volume and during the process, there is fall of temperature to 15°C The work done during the process is 52.5 kJ. Calculate Cp and Cv.
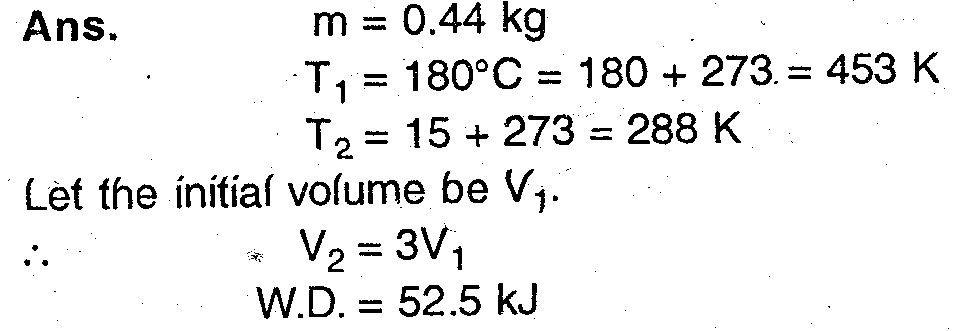
For an adiabatic process
Taking log on both sides
R = 0.296 kJ/kg K
also we know that
Cp – Cv = R
1.41 Cv – Cv = 0.296
Cp = 1.41 x 0.72 = 1.015kJ/kgK
Q 11. What is an isochoric process? Show it on P-V diagram and explain the various property changes.
Ans. Fig. 13 (a) shows a completely closely filled vessel with a perfect gas being heated from outside. It results in increase in pressure and temperature of system.
This is represented on P-V diagram. Fig. 13 (b)
Let Q heat be supplied during the process in which system changes its properties from state (1) and state (2)
Since there is no expansion of gas, no work (mechanical) is being done by the system. This also clear that the area under the pressure volume curve is zero
Therefore all of heat supplied is stored in system.
The heat supplied to unit mass of gas at constant volume is = Cv dT ……(2)
from (1) and (2)
and H2 — H1 = mCp (T2 — T1) = Change in enthalpy.
Q12. A quantity of air at 1 bar and 7°C is heated at constant volume in a cylinder until its temperature has risen to 827°C. After this it is expanded isentropically until the temperature is again equal to 7°C. Determine, per kg of air,
(a) pressure, volume and temperature at the end of each of the operations
(b) the heat input to cycle
(c) work output of cycle
(d) efficiency of cycle
From characteristics gas equation,
For constant volume process 1—2
Heat supplied = mCv (T2 — T1)
= 1 x 0.718(1100—280)
Q = 5888.70 kJ/kg
For isentropic process (expansion)
Q.13 During a non flow frictional less compression process, the volume changes from 0.12 m to 0.04 m and system rejects 40 kJ of heat. Determine the change in internal energy, heat loss and enthalpy if pressure varies with volume as (bar) = 4.5 (v) + 2; where v in m and internal energy is given by the equation = 40.— p (bar). v (m).
Solution. V1 = 0.12 m
V2 = 0.04m
Q = — 40kJ
P = 4.5V + 2, U = 40 — pV
W.D. = — 18.8 kJ
Change in internal energy
Q.14. 1Kg of air at 3.5 bar and occupying 0.35 m3 is heated at constant volume until its temperature has risen to 316°C Find
(a) Initial temperature of air
(b) the final pressure of air V
(c) heat added
(d) gain in internal energy per Kg. V
Take Cv = 0.715 KJ/Kg K.
Ans m = 1Kg
Initial temperature of air
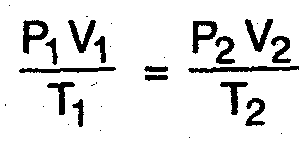
if air is heated at constant volume,
Final pressure at air:
Heat added:
= 1 x 0.715 (589 — 412)
=106.555 KJ
(d) Gain in internal energy:
dU = = 106555 KJ.
